How Many Games?

A joke is told about mathematicians:  If you show a mathematician a pot of water on the kitchen table, and ask him to please boil the water, he will gladly place it on the stove and heat it up to boiling.  If you then, perhaps the next day, show him a pot of water on the kitchen counter, and ask him to please boil the water, he will then place the water on the table.  After all, reasons the mathematician, he has merely reduced the problem to one he has already solved.

I didn't say it was a funny joke. Still, I like it.  And it is vaguely related to the concept of recursion,which comes in handy for finding out the about the number of games possible in the Sim universe.

When Simmons first proposed Sim, he conjectured that the second player might have an advantage, since the first player can draw up to eight lines, while the second player can draw only seven.  Ignoring the first four lines--since it is impossible for a player to make a single-color triangle until he has drawn three lines--the first player has five chances to lose as opposed to the second player's four chances.  Simmons figured this is likely an advantage, as a player doesn't so much win in Sim as he avoids becoming the loser--the game ends when one player forms a triangle entirely of his color. Therefore, a winning strategy really involves "not losing."

To test Simmons' conjecture, we use a computer program to iterate through each of the different possible games, and then count which of them end after an odd or even number of lines, which corresponds to a loss for Player One or Player Two.

Lines Drawn     End Games
1 line:                 0
2 lines:                0
3 lines:                0
4 lines:                0
5 lines:           15,840
6 lines:          151,200
7 lines:        4,082,400
8 lines:       27,993,600
9 lines:      348,364,800
10 lines:   1,488,067,200
11 lines:   9,068,112,000
12 lines:  19,719,936,000
13 lines:  45,816,192,000
14 lines:  28,086,912,000
15 lines:   4,572,288,000

Table 2-1

 

Player One can lose with 5, 7, 9, 11, 13, or 15 lines, while Player Two can lose with 6, 8, 10, 12, or 14 lines. Apparently, Player One loses in 59,809,055,040 games, while Player Two loses in 49,323,060,000 games, which seems to confirm that Player Two has an advantage.  The total number of games in the Sim universe is 109,132,115,040.

It is interesting to me that there are some 15,000 games that end after five lines (the shortest game possible).  This could only happen if Player One was being completely contrary and trying to lose.

 

Figure 2-1

What if we somehow take out such premature losses, and only count those that are forced?

Let us try to refine the definition of Sim in the following way:  Players alternate drawing lines as before, except that completing a single-colored triangle is now an illegal move.  The last player to draw a line--to bring the game to the point where no more legal lines may be drawn--is declared the winner.  In this version, which I will call Sim+, the numbers turn out a little differently:

Lines Drawn     End Games
1 line:                 0
2 lines:                0
3 lines:                0
4 lines:                0
5 lines:                0
6 lines:                0
7 lines:                0
8 lines:                0
9 lines:           86,400
10 lines:      27,993,600
11 lines:     248,832,000
12 lines:   6,625,152,000
13 lines:  11,757,312,000
14 lines:   4,572,288,000
15 lines:               0

Table 2-2

This time, Player One wins with 9, 11, or 13 lines (no one can get to 15 lines--it would cause an illegal move) while Player Two wins with 10, 12, or 14 lines.  Doing the math, Player One wins 12,006,230,400 different games, while Player Two wins "only" 11,225,433,600 games (a total of 23,231,664,000--only 20% of the games in regular Sim).  So, maybe when the players actively avoid making the final triangle (or, as in Sim+, it is illegal to do so), then Player One has the advantage, or at least the game is a lot more evenly matched.  It's interesting to me that in both games, the maximum number of end games occurs at 13 lines.  For Sim+, this helps Player One's win totals tremendously; for regular Sim, it is a detriment.

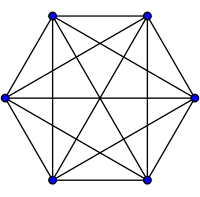
As opposed to regular Sim, the first end game in Sim+ occurs at 9 lines, a win for Player One, since Player Two cannot avoid making a triangle.  What does this look like?  Here's an example (I think it has a nice symmetry):

  

Figure 2-2

In order to generate the numbers for the tables above, I initially wrote a simple recursive program (a "depth-first" search in computer terms).  However, it was taking a really long time. How long?  I'm glad you asked.  I recorded some numbers on the second table (the smaller of the two), and finally quit after the program had run for six and a quarter hours.  At that point, we were about 3.8% of the way through the process, which implies it would have taken just a few hours short of a week to finish the calculations.  I ended up calculating the tables a different way, which I hope to tell about in another entry.